graphs
— 2019-04-22
- You, sobbing: You can't just point at every data structure and call it a graph.
- Me: *pointing at a linked list*: graph.
— @mgattozzi (paraphrased)
Graphs are a bit of an umbrella term in the field of data structures. There are many kind of graphs, and each has different properties. Inherently graphs are about expressing relationships, and understanding what the relationships of a problem are can help you understand the fundamental structure of a problem. Which in turn provides you with the right starting point to simplify a problem.
In this post we'll briefly go through some common graph types, their properties, and examples of problems that can be expressed in them.
Primer
Before we dive in, it might be useful to (re-)explore some basic concepts related to graphs. Feel free to skip this if you're already comfortable with them, but perhaps this might be useful regardless.
Relationships
Any kind of relationship can be expressed as one of 3 kinds:
- 1 to 1 relationship (aka
1:1) - 1 to many relationship / many to 1 relationship (aka
1:m,m:1) - many to many relationship (aka
m:n)
Graphs
A graph structure is one of "nodes" and "relationships between nodes". This is often also referred to as "vertices and edges" (vertices is a plural of "vertex").
Graphs are a really good structure to express "things" and "relationships between things". If this sounds general, it's because it is! A lot problems can be expressed in terms of graphs, which is why it's such a useful structure to be comfortable with!
Some types of graphs not only store data on the nodes, but on the edges too. But if you ever happen to read up on "graph databases" you might see words such as "triples" and "quads" come by.
"triples" means there's 1 slot to store data per relationship, and "quads" means there's two slots
to store data per relationship (e.g. a distinction between A -> B and A <- B). But none of that
matters for this post.
Cycles
If you've read about graphs, you might've seen the words "acyclic", "cyclic" or "cycles" come by. This refers to whether or not a graph structure's relationships can be followed to create loops.
For example a relationships of A -> B -> A is cyclic. And so is A -> B -> C -> A. Even if loops
don't naturally occur in a structure, it can still be "cyclic" if there's the possibility of them
occurring in the future. If the structure guarantees no loops can ever occur, it's referred to as
"acyclic" (non-cyclic).
directed graphs
Properties
| Property | Value |
|---|---|
| Cycles | Possible |
| Max children per node | Unconstrained |
| Max parents per node | Unconstrained |
About
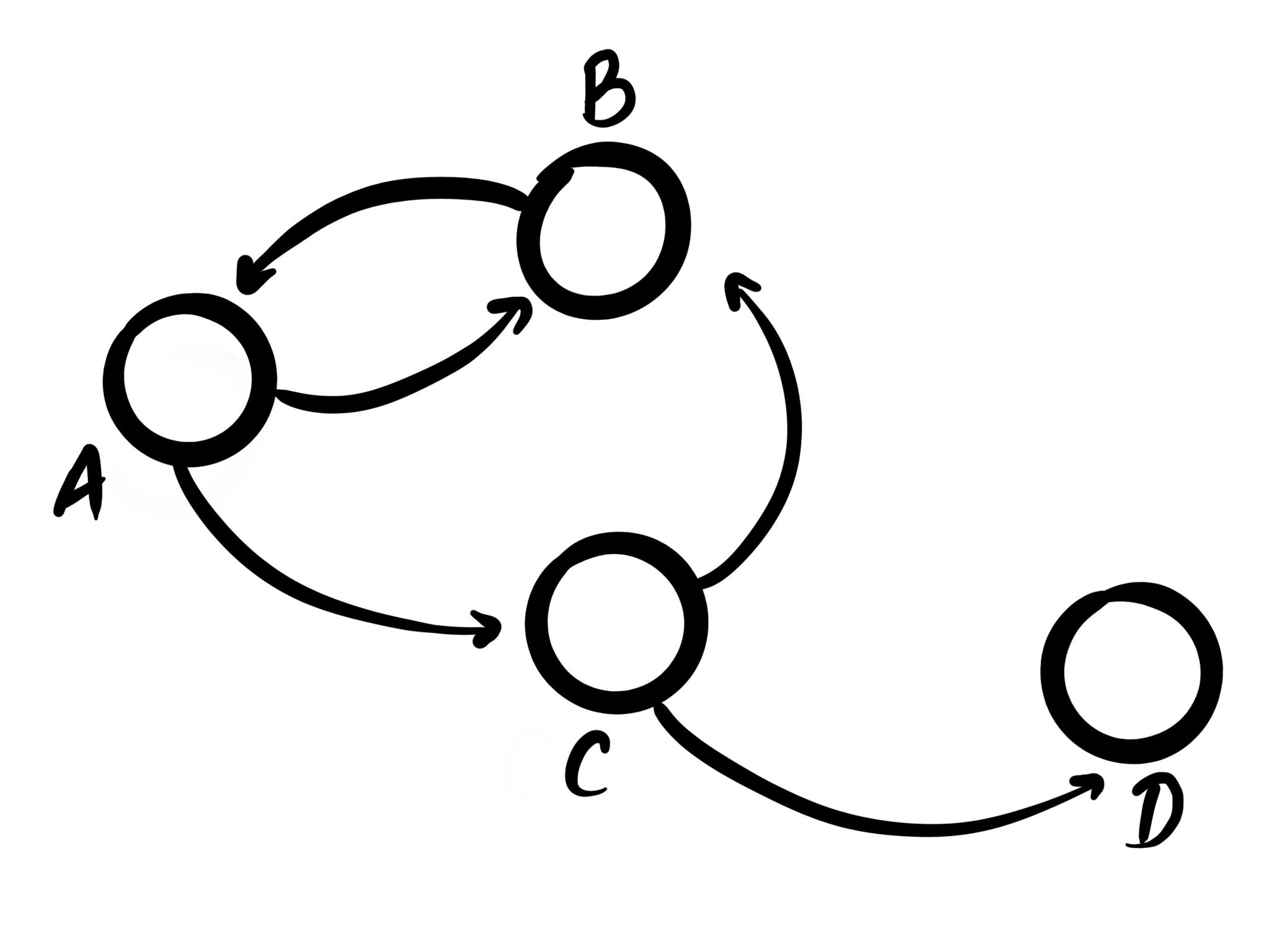
The most basic of types is the (cyclic) graph. This type of graph has the fewest constraints, and is
what people usually refer to when they talk about "graphs". Every node can have an m:n
relationship, and nodes can sometimes even link to themselves directly.
In this kind of generic graph, any connection is allowed. This can make it hard to keep track of, as when any new connection is added, all assumptions about the graph might have changed, which means that to draw make any meaningful statements about it, the whole graph needs to be re-evaluated.
These types of graphs are the most flexible, but also provide the fewest guarantees.
Examples
Probably the most common example here is that of a social network. Any person can have a relationship with any other people, and there's no constraint on who they are, and how many relationships there can be.
acyclic graphs
Properties
| Property | Value |
|---|---|
| Can have cycles | No |
| Max children per node | Unconstrained |
| Max parents per node | Unconstrained |
About
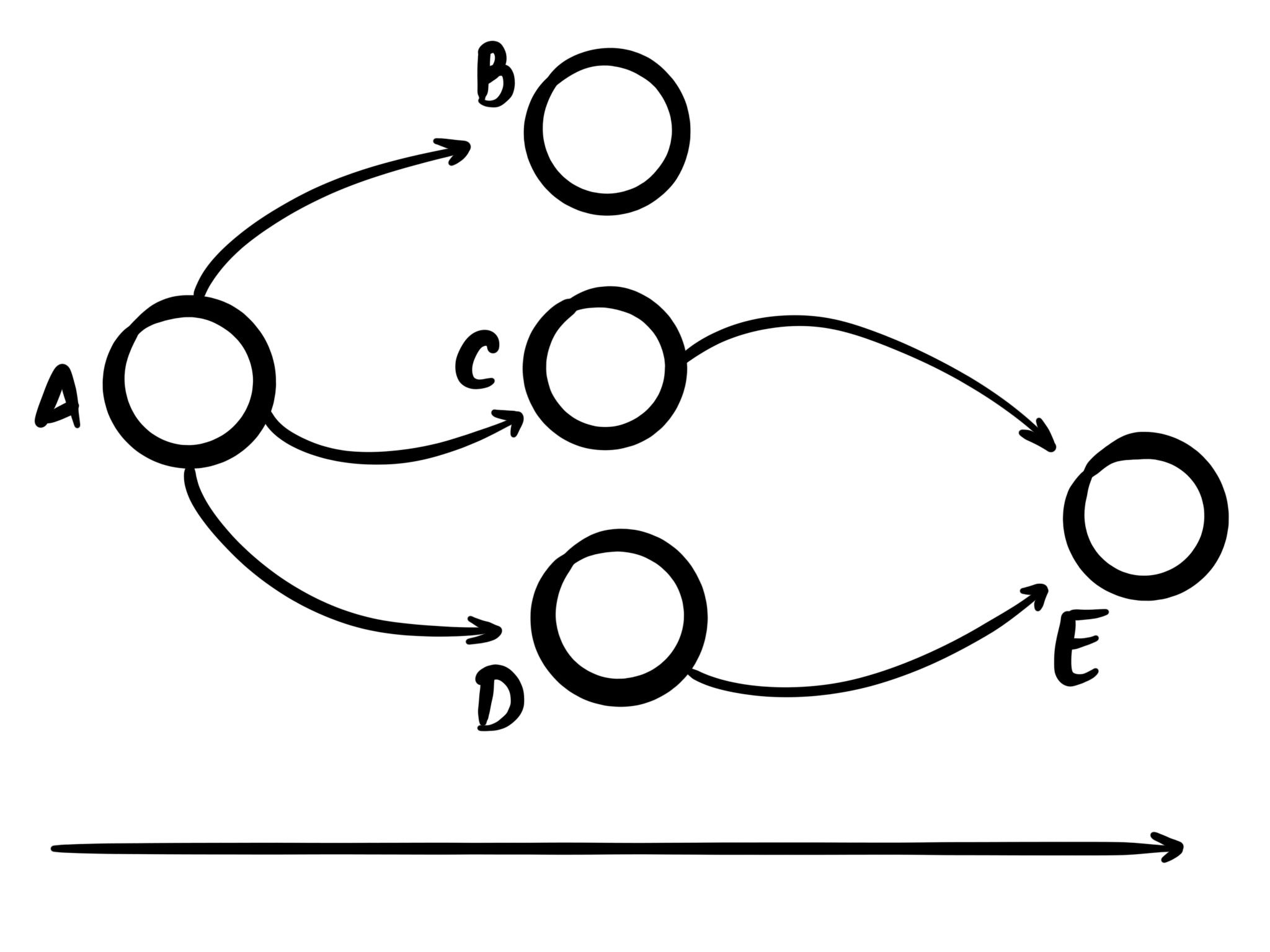
An acyclic graph is similar to a regular graph, but unlike a regular graph it can't contain cycles. This is useful when using computers to guarantee no infinite loops can occur. For example when building message-based systems, having a guarantee that no infinite loops can occur can help with inter-system reliability.
The way acyclic graphs are defined is usually by establishing a hierarchy of "parent nodes" and
"child nodes". In the image above [B, C, D] are children of A, and A is the parent of [B, C, D].
The way cycles are prevents is by roughly applying the following rules to the graph:
- any node can have multiple parent nodes
- any node can have multiple child nodes
- a parent or sibling node can't also be a child node
This is a simplification of the full set of rules, but the general idea should translate. But acyclic graphs already provide a lot more guarantees than general graphs!
Examples
A common example you'll encounter is that of software dependencies. Any dependency can have any other dependencies, but if there's cycles in the dependency graph it can't resolve (e.g. you can't dependency of yourself).
Trees
Properties
| Property | Value |
|---|---|
| Can have cycles | No |
| Max children per node | Unconstrained |
| Max parents per node | 1 |
About
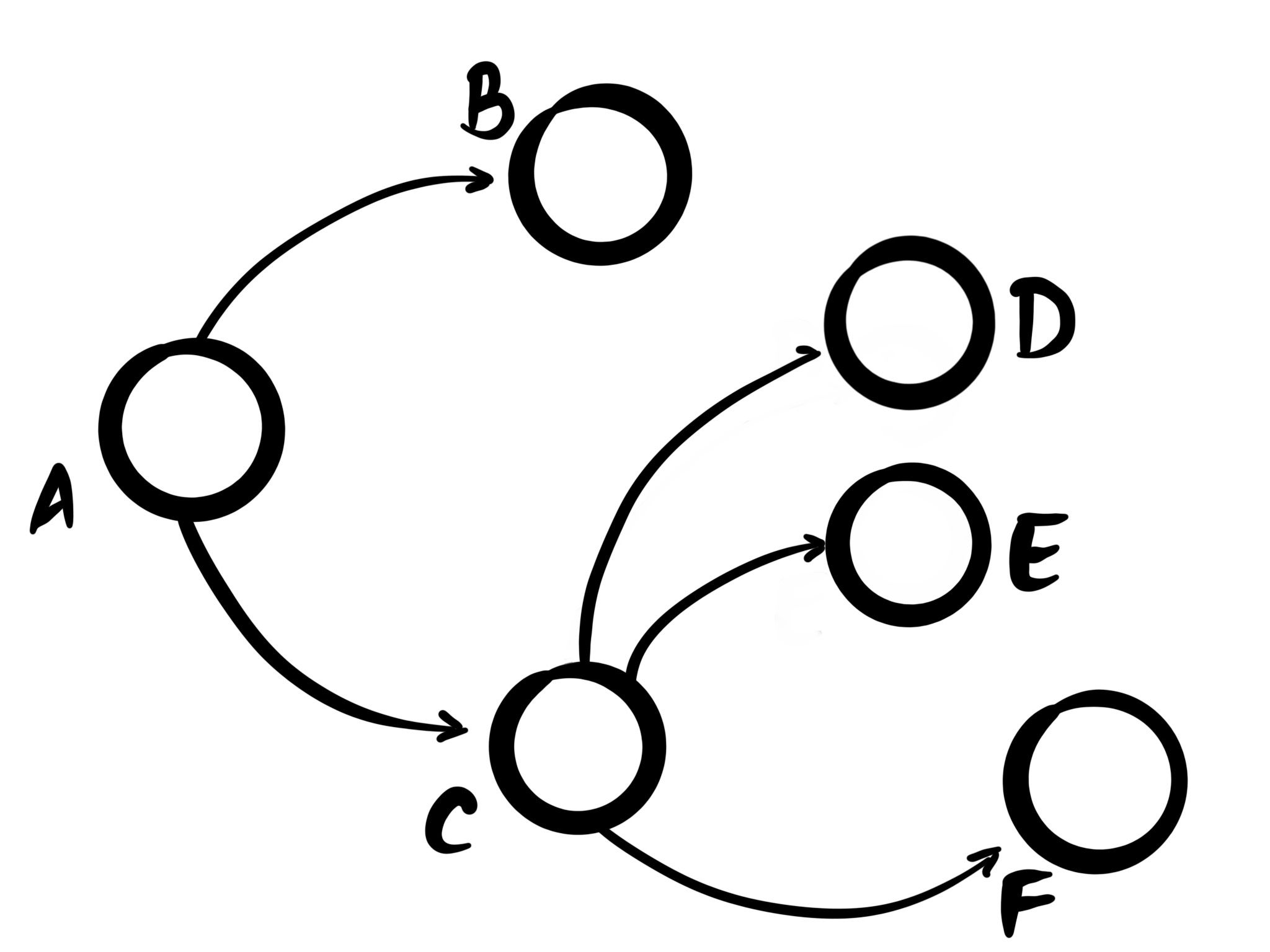
Trees are a simplification of acyclic graph. They impose an additional constraint that each node must have exactly one parent (except for the root node, which has none).
A well-known subtype of trees is that of "binary trees" where each node may have up to 2 children.
Examples
Rust's data model is an example of a tree. Any piece of data must have exactly one parent, but can share references to multiple child functions. The child functions can't outlive the lifetime of the parent, essentially creating a tree. This is as opposed to for example C, where what you want is for the memory to be expressed as a tree, but the language allows you to express it as a directed graph.
Similarly function execution forms a tree, where any function can call multiple functions, but no single function call ever originates from two callers at the same time, always creating a tree. The topic of structured concurrency covers this well. The Tl;Dr being: if you can express concurrency as a tree, it's a lot easier to reason about. And the same applies to error handling too. Oh, and HTML.
Logs
Properties
| Property | Value |
|---|---|
| Can have cycles | No |
| Max children per node | 1 |
| Max parents per node | 1 |
About
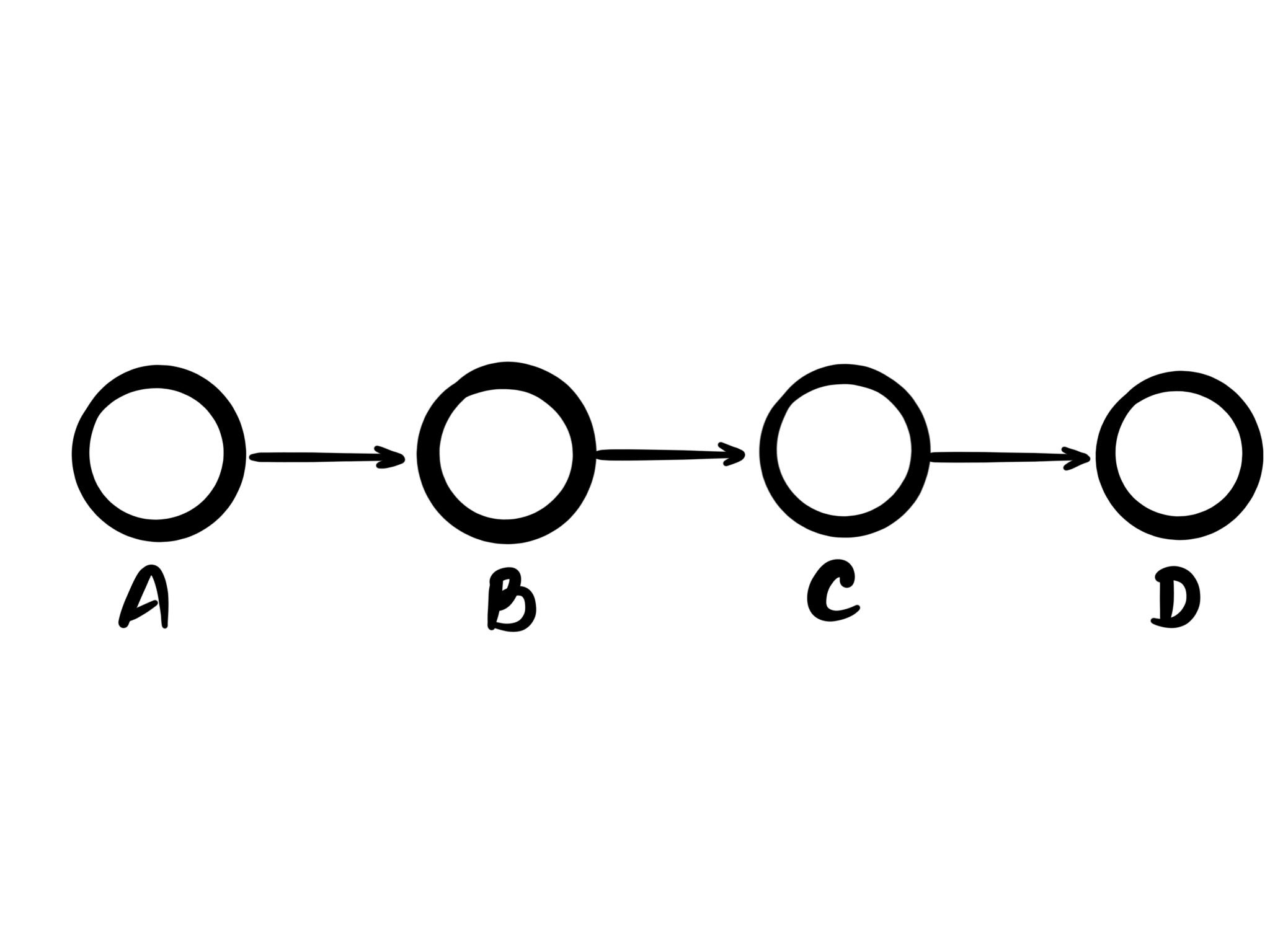
Logs (or lists) are probably the simplest kind of graph out there. Every node has one parent, and at most one child (except for the root node). One of the most interesting properties they have is that they provide absolute ordering of the items in them, meaning there's never a question which entry came before which other entry.
Examples
Logs are widely applicable. The most common use is probably as "arrays" in programming language, or sequences of bytes in memory. But for databases lists are fantastic as a model to track events in that can be processed and replayed into more types that can be queried.
Logs are generally used for anything involving time too. For example in accounting data is tracked as a series of events where money goes in, and money goes out. And anything commonly referred to as a "feed" also tracks data over time.
Logs are everywhere, and despite their relatively simple nature, a lot of problems can be expressed as a log.
Conclusion
In this post we've talked about different types of graphs, their properties, and examples of them. This an example of the idea of "more constraints can be better".
Something I haven't mentioned is how well some graph types map to data visualizations. In particular trees can be visualized nicely as either a flame chart, flame graph, or flame scope.
Thanks for reading!
Thanks
Thanks to @_lrlna for helping create the illustrations, and helping bounce ideas off of!